
As a member of "Scientists for Future, group Tübingen" I support "Fridays for Future".
I believe that scientists have particular responsibility to
- point out that climate change is human made and dangerous
- reduce greenhouse gases of scientific business, see our petition
- point out that serious political and economic changes are needed to mitigate climate change
- point out that reacting to climate change is needed despite all efforts
- spread the belief that also fascinating scientific questions are raised by these problems
Since 2003, I work on causal inference from statistical data and the foundation of new causal inference rules. From 1995 to 2007, I worked on quantum information theory, quantum computing, complexity theory, and thermodynamics. This work can be summarised as physics of Information and I think that causal inference also relies on assumptions that connect physics with information (see the following section). I believe that the science of causality is "abstract physics"
My complete list of publications can be found here. Our recent book on causal inference can be bought or downloaded here (It has been awarded the ''Causality in Statistics Education Award 2018'').
Asymmetry between past and future in physics: Consider the following sequence of images: a beam of particles approaches an object with some non-trivial structure. Each particle is scattered at the object and thus bounces in a different direction. The outgoing particles thus contain information about the object (see our book for details).
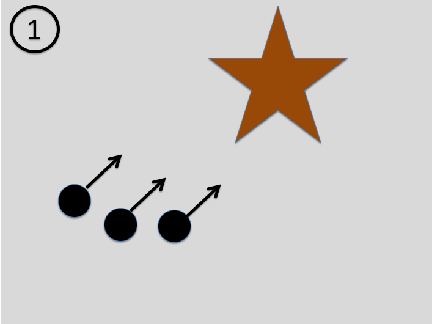

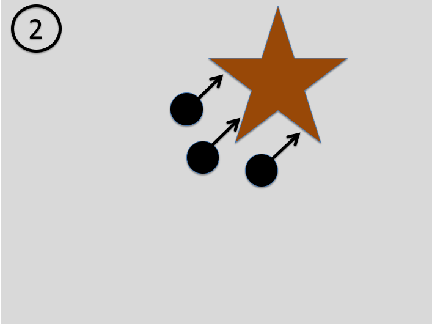

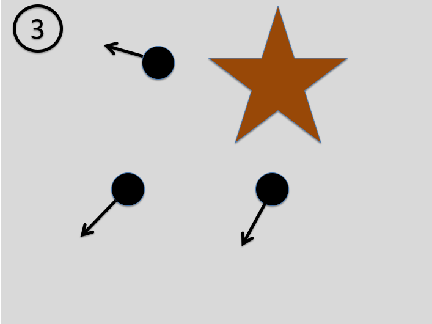
If the scattering process has been perfectly elastic, that is, the outgoing particles have the same speed, the laws of physics also allow for the time inverted scenario: The particles approach the object from different directions, but the outgoing particles form a beam whose particles all move in the same direction:
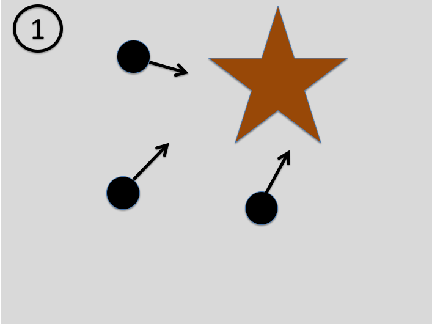

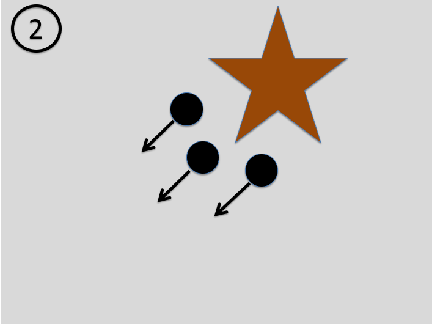

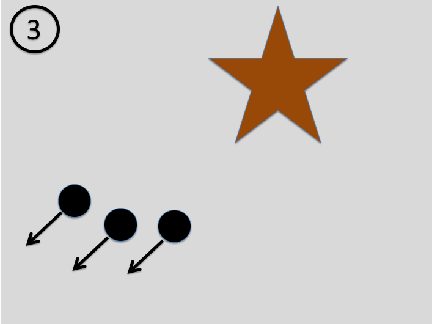
Although this scenario is in principle possible, the first one is much more plausible. What makes the second one implausible is that the positions and velocities of the incoming particles need to contain information about the object to all fly in the same direction after being scattered at the object. It thus requires some rather sophisticated tuning of the initial state of the particles. It is unlikely that a beam contains information about an object before hitting it and loses this information in the scattering process. For the same reason, photographic images show the past and not the future because the photons (‘light particles’) contain information about an object after hitting it.
Asymmetry between cause and effect in statistics: In analogy to the above asymmetry, there are joint distributions P(X,Y ) of two variables X,Y for which one causal direction is more plausible than the converse direction. In principle, one can always generate P(X,Y ) in the following two ways:
(1) first generate X according to P(X) and then generate Y according to P(Y |X)
(2) first generate Y according to P(Y ) and then generate X according to
P(X|Y )
For the following example scenario (2) is more plausible. Let Y be a real-valued variable whose distribution is Gaussian. Let X be a binary variable that attains the value 0 whenever Y attains a value below a certain threshold y0, whereas X attains 1 above whenever Y > y0.
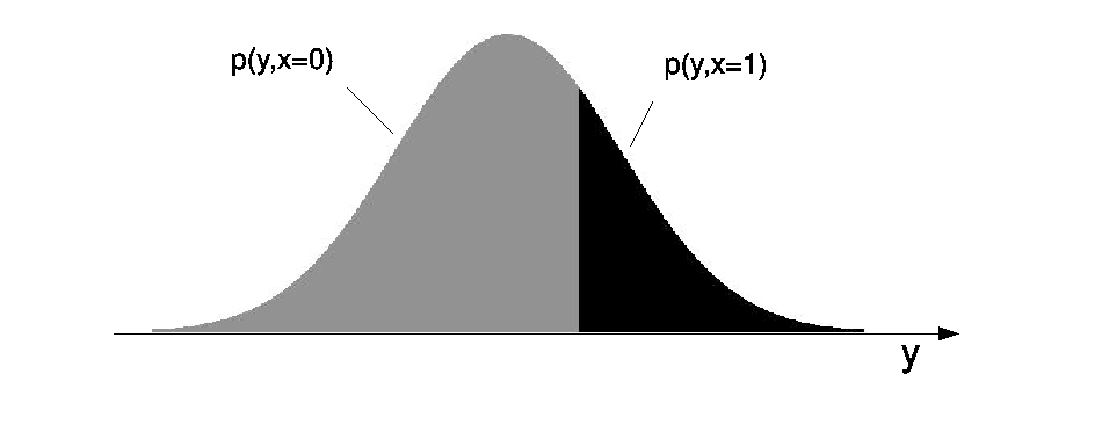
The causal hypothesis ‘Y causes X’ is quite plausible because one can easily think of a mechanism whose output X depends on whether Y is above y0 or not. Consider, on the other hand, the hypothesis ‘X causes Y ’. It requires a mechanism with binary input X. Depending on whether X attains 0 or 1, the mechanism outputs Y -values whose distribution is the black or the grey truncated Gaussian. Apart from the fact that this is already a rather contrived mechanism, there is also something about this causal hypothesis that is even more disturbing: the input distribution P(X) seems to be ‘fine-tuned’ to generate an output that is Gaussian. This is because generic input distributions P(X) yield distributions like this (images taken from here):
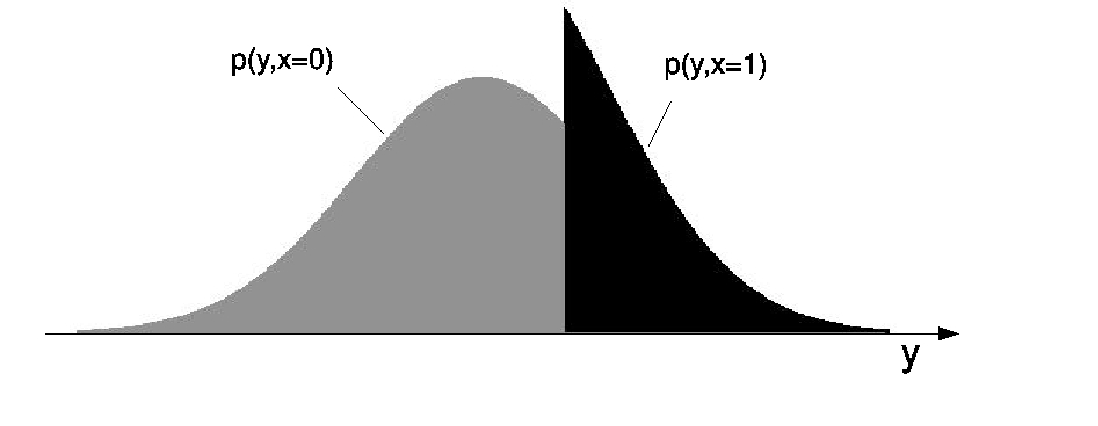
The common root: In a physics paper we have explained the common principle behind the asymmetry between past and future in the scattering scenario and the asymmetry between cause and effect in the statistical scenario: We have postulated that typically the initial state and the mechanism that maps the initial state to the final state contain no information about each other, where ‘no information’ is meant in the sense of algorithmic information (two objects are said to be algorithmically independent if the description of one object does not get shorter when the other object is known). The beam contains no information about the object (the mechanism that maps the input to the output beam). Likewise, the input Pcause) contains no information about the mechanism P(effect|cause) relating cause and effect. Therefore, we can reject the hypothesis ‘X causes Y ’ because, given P(Y |X), the marginal distribution P(X) has a short description as ‘the unique distribution for which the output distribution P(Y ) is Gaussian.’